پس انتشار قسمت دوم
به یاد بیاورید که تابع هزینه برای یک شبکه عصبی به این صورت بود:
$$ \begin{gather*}J(\Theta) = - \frac{1}{m} \sum_{t=1}^m\sum_{k=1}^K \left[ y^{(t)}_k \ \log (h_\Theta (x^{(t)}))_k + (1 - y^{(t)}_k)\ \log (1 - h_\Theta(x^{(t)})_k)\right] + \frac{\lambda}{2m}\sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_l+1} ( \Theta_{j,i}^{(l)})^2\end{gather*} $$
اگر یک طبقه بندی ساده، و غیر چند کلاسه ($k=1$) را در نظر بگیریم و همچنین منظم سازی را هم نادیده بگیریم، تابع هزینه ما به این صورت محاسبه خواهد شد:
$$ cost(t) = y^{(t)} \log(h_\Theta(x^{(t)})) + (1 - y^{(t)}) \log(1 - h_\Theta(x^{(t)})) $$
واضح است که $\delta^{(l)} _j$ به عنوان خطا برای $a^{(l)} _j$ است (گره $j$ ام در لایه $l$).
به طور رسمی تر، مقادیر دلتا در واقع مشتق تابع هزینه هستند: $$ \delta^{(l)} _j = \frac{\delta}{\delta z_j ^{(l)}} cost(t) $$
به یاد آورید که مشتق ما شیب یک خط مماس با تابع هزینه است، بنابراین هرچه شیب بیشتر باشد، بیشتر در اشتباه هستیم.
بیایید شبکه عصبی زیر را در نظر بگیریم و ببینیم که چطور میشود برخی از $\delta^{(l)} _j$ ها را محاسبه کرد:
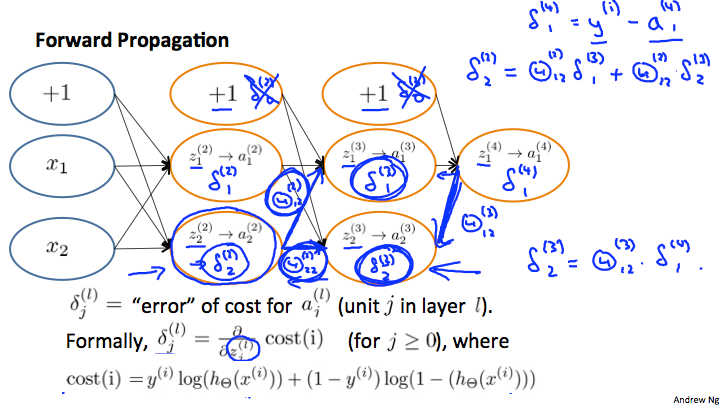
در تصویر بالا برای محاسبه $\delta^{(2)} _2$ (بالا سمت راست تصویر) وزن های $\Theta ^ {(2)} _{12}$ و $\Theta ^ {(2)} _{22}$ را با هم ضرب کرده ایم، و مقادیر $\delta$ مربوطه نیز در سمت راست هر کدام از آن ها وجود دارد، که بنابراین خواهیم داشت: $$ \delta^{(2)} _2 = \Theta ^ {(2)} _{12} \ast \delta^{(3)} _1 + \Theta ^ {(2)} _{22} \ast \delta^{(3)} _2 $$
برای محاسبه هر کدام از $\delta ^ {(l)} _j$ های ممکن، میتوانیم از سمت راست نمودار شروع کنیم، تصور میکنیم که جهت $\Theta _ {ij}$ هایمان از سمت راست به چپ است، و برای محاسبه هر $\delta ^ {(l)} _j$ فقط باید جمع همه وزن ها را در مقدار $\delta$ ای که از آن جا آمده اید ضرب کنید.
به همین شکل یک مثال دیگر میتواند به این صورت باشد: $$ \delta ^ {(3)} _2 = \Theta ^ {(3)} _{12} \ast \delta^{(4)} _1 $$