تابع هزینه
ما نمیتوانیم از همان تابعی هزینه ای که برای رگرسیون خطی استفاده کردیم، برای تابع لجستیک نیز استفاده کنیم، زیرا خروجی تابع لجستیک موج گونه است و باعث ایجاد تعداد زیادی مینیمم محلی میشود. به عبارت دیگر یک تابع محدب نیست.
تابع هزینه ما برای رگرسیون لجستیک به این صورت است:
$$ J(\theta) = \frac{1}{m} \sum_{i = 1}^m Cost(h_\theta(x^{(i)}, y^{(i)})) $$
$$ Cost(h_\theta(x), y) = -log(h_\theta(x)) \hspace{1cm} if \hspace{0.3cm} y = 1 $$
$$ Cost(h_\theta(x), y) = -log(1 - h_\theta(x)) \hspace{1cm} if \hspace{0.3cm} y = 0 $$
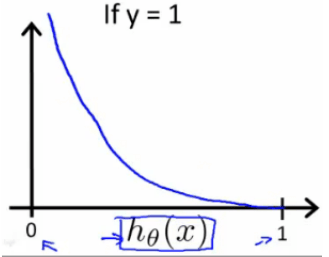
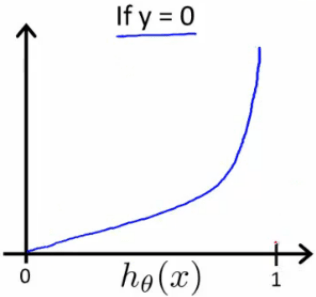
هرچه تابع فرضیه از $y$ دور تر باشد، خروجی تابع هزینه بزرگ تر است.
و اگر تابع فرضیه برابر با $y$ باشد، هزینه ما $0$ است.
$$ Cost(h_\theta(x), y) = 0 \hspace{0.3cm} if \hspace{0.3cm} h_\theta(x)) = y $$
$$ Cost(h_\theta(x), y) \rightarrow \infty \hspace{0.5cm} if \hspace{0.3cm} y = 0 \hspace{0.3cm} and \hspace{0.3cm} h_\theta(x) \rightarrow 1$$
$$ Cost(h_\theta(x), y) \rightarrow \infty \hspace{0.5cm} if \hspace{0.3cm} y = 1 \hspace{0.3cm} and \hspace{0.3cm} h_\theta(x) \rightarrow 0 $$
اگر پاسخ صحیح ما $y = 0$ باشد، سپس تابع هزینه $0$ خواهد شد، اگر خروجی تابع فرضیه ما نیز $0$ شود.
اگر فرضیه ما به $1$ میل کند، سپس تابع هزینه به بی نهایت میل میکند.
اگر پاسخ صحیح ما $y = 1$ باشد، سپس تابع هزینه $0$ خواهد شد، اگر خروجی تابع فرضیه ما $1$ شود.
اگر فرضیه ما به $0$ میل کند، سپس تابع هزینه به بی نهایت میل میکند.
به خاطر داشته باشید که نوشتن تابع هزینه به این روش که $J(\theta)$ برای رگرسیون لجستیک محدب است.