معادله نرمال
معادله نرمال
الگوریتم گرادیان کاهشی روشی بود برای مینیمم کردن تابع $J$ ، اما روش دومی نیز وجود دارد که بدون داشتن حلقه تکرار این کار را انجام بدهد که معادله نرمال نام دارد.
فرض کنید که تابع هزینه درجه دو ای مثل این داریم: $$ J(\theta) = a\theta^2 + b\theta + c $$ $$ \frac{\partial} {\partial x} J(\theta) \overset{\underset{\mathrm{set}}{}}{=} 0 $$
که برای مینیمم کردن این تابع درجه دو مشتق آن را میگیریم و برابر با 0 قرار میدهیم، که این به ما اجازه میدهد که مقدار $\theta$ را برای مینیمم کردن تابع پیدا کنیم.
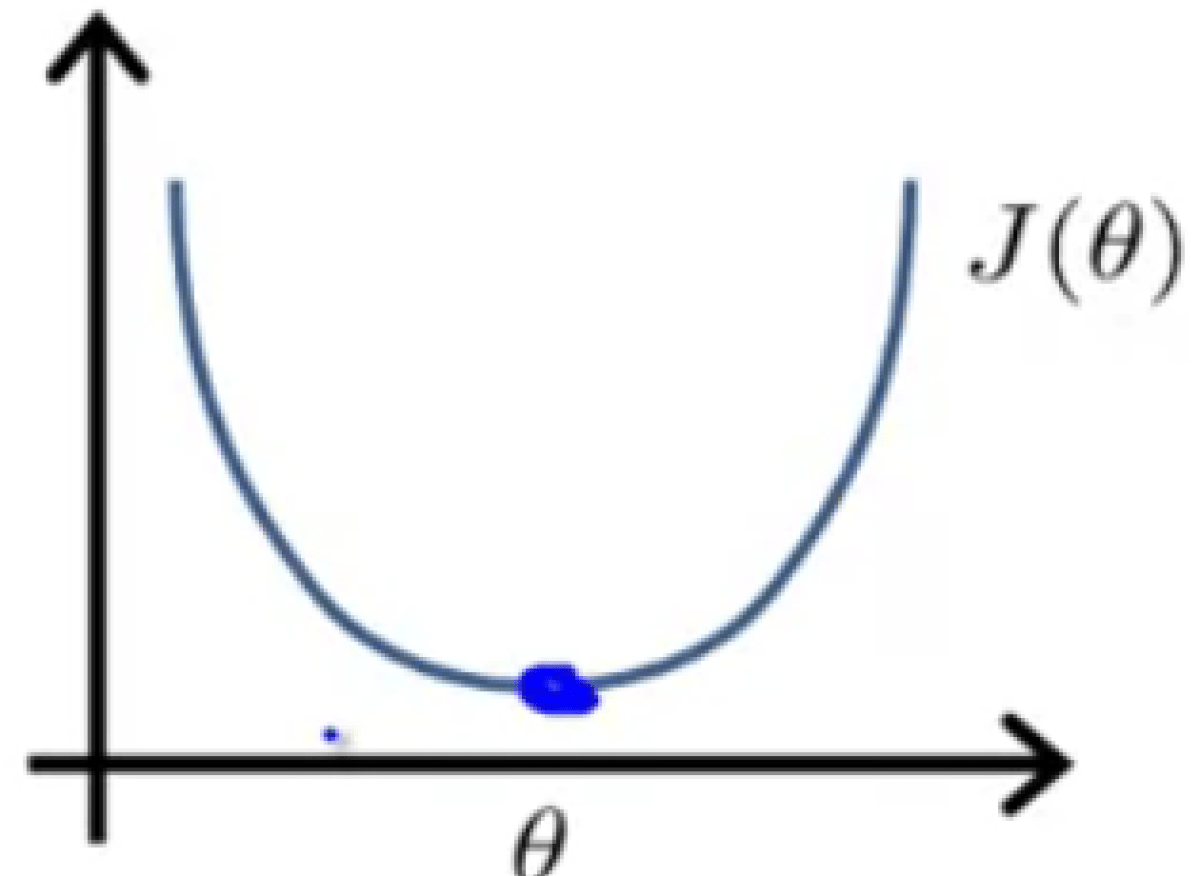
اما مسئله ای که برای ما جالب است $\theta$ یک عدد حقیقی نیست، بلکه یک بردار در ابعدا 1+n است:
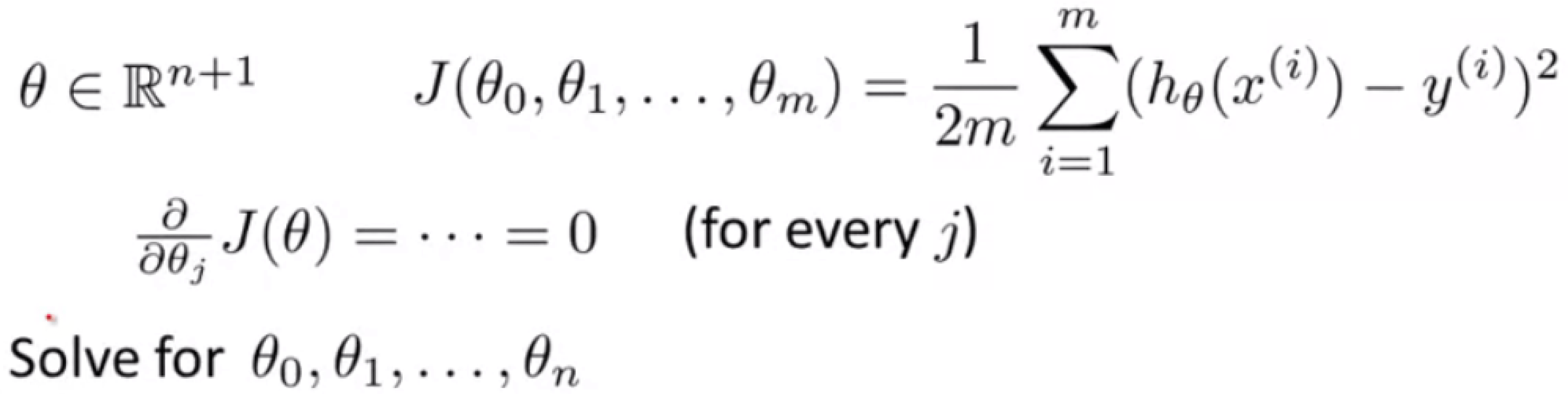
برای محاسبه اینکه چطور تابع هزینه را مینیمم کنیم باید مشتق جزئی تابع $J$ را برای هر کدام از تتا ها بگیریم و برابر با 0 قرار دهیم، بعد از محاسبه همه معادله ها مقدار تتا ای که تابع $J$ مینیمم میشود را به دست میآوریم.
اگر مجموعه آموزشی به این شکل داشته باشیم:
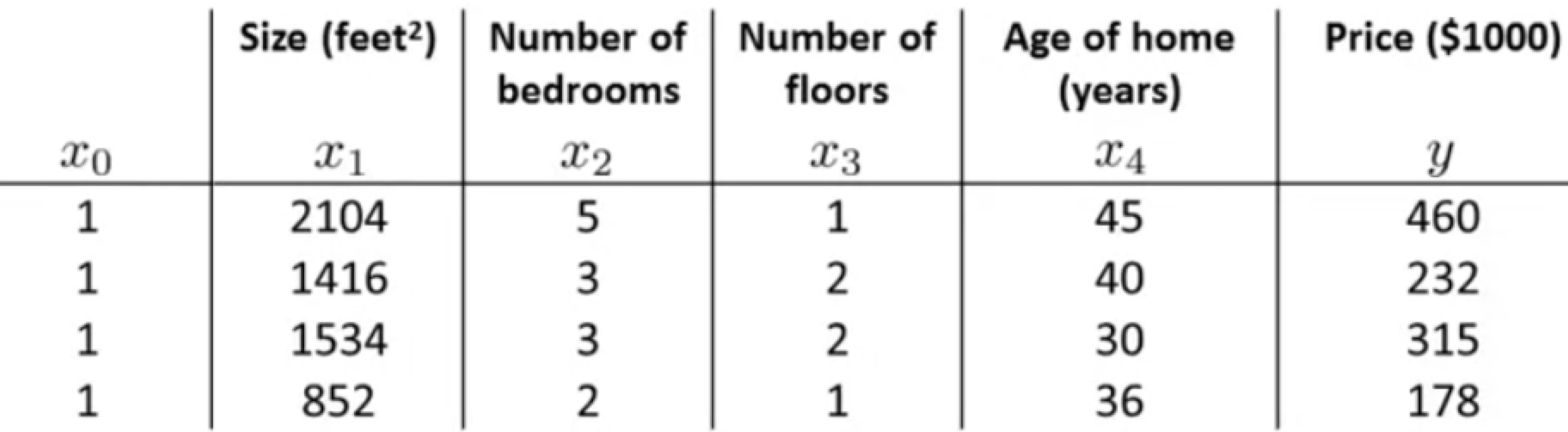
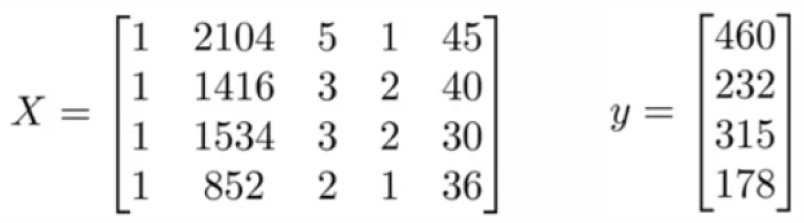
معادله نرمال ما برای محاسبه تتا به این صورت خواهد بود:
$$ \theta = (X^T X)^{-1} X^T y $$
با استفاده از معادله نرمال نیازی به مقیاس بندی ویژگی نداریم، و برای مقایسه گرادیان کاهشی و معادله نرمال:
| گرادیان کاهشی | معادله نرمال |
|---|---|
| به تنظیم پارامتر آلفا نیاز دارد | به تنظیم پارامتر آلفا نیاز ندارد |
| به تکرار نیاز دارد | به تکرار نیاز ندارد |
| مرتبه زمانی اش $O(kn)^3 $ است | مرتبه زمانی اش $O(n)^3$ است |
| برای تعداد ویژگی های زیاد خوب کار میکند | برای تعداد ویژگی های زیاد کند است |